Matematicas Discretas - Relaciones de recurrencia

Relaciones de recurrencia

Una relación de recurrencia para la secuencia {an} es una ecuación que expresa an en términos de uno o

mas de los términos previos de la secuencia (a0, a1, ....., an-1), para todos los enteros n con n≥n0, donde n0 es un entero no negativo. Una secuencia es llamada una solución de una relación de recurrencia si sus términos satisfacen la relación de recurrencia.

$a_n = P_1(n)(x_1)^n+P_2(n)(x_2)^n + cdots + P_s(n)(x_s)^n$

Solucion de una relacion de recurrencia

Una relación de recurrencia de grado k con coeficientes constantes es una relación de recurrencia de la forma: an= c1an-1 + c2an-2 + …. +ckan-k . Donde c1, c2, …. ck son números reales, y ck≠0. Nota: la relación de recurrencia en la definición es lineal puesto que el lado derecho es una suma de múltiplos de los términos previos de la secuencia. Es homogénea puesto que ninguno de los términos no son múltiplos de los aj .(Los coeficientes de los términos son todos constantes (no dependen de n .El grado es k porque es expresada en términos de los k términos previos de la secuencia.

Solucionando ecuaciones de recurrencia homogéneas con coeficientes

constantes

La primera alternativa consiste en buscar soluciones de la forma an= rn , donde r es una constante. Note que an=rn es una solución de la relación de recurrencia an=c1an-1+c2an-2+ …. +ckan-k si y solo si: rn=c1rn-1+c2rn-2+ …. +ckrn-k. Cuando dividimos ambos lados por r n-k y reacomodamos para que la ecuación resultante sea igualada a 0, obtenemos la siguiente ecuación: rk- c1rk-1- c2rk-2- …. - ck-1r - ck = 0. (ecuación característica) Consecuentemente, la secuencia { an } con an= rn es una solución si y solo si r es una solución de la ecuación característica. Las soluciones de esta ecuación son llamadas las raíces características de la relación de recurrencia.

Una relación de recurrencia lineal no homogénea con coeficientes constantes, es una relación de la

forma:

an=c1an-1+c2an-2+ …. +ckan-k + F(n). Donde c1, c2,....,ck son números reales y F(n) es una función no

igual a 0 que depende solo de n. la relación de recurrencia:

an=c1an-1+c2an-2+ …. +ckan-k es llamada la relación de recurrencia homogénea asociada.

Ejemplo

Ejemplo : Números de Fibonacci

Los números de Fibonacci están definidos usando la siguiente relación de recurrencia lineal:

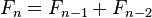
$F_{n} = F_{n-1}+F_{n-2} ,$

con los valores iniciales:

$F_1 = 1 ,$

$F_2 = 1 ,$

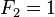
La secuencia de los numeros de Fibonacci comienza: 1, 1, 2, 3 ,5, 8, 13, 21 ,34, 55, 89... El objetivo de la resolución de la ecuación de recurrencia es encontrar una forma cerrada para calcular los números de Fibonacci.

La ecuación característica es la siguiente:

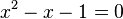
$x^2 - x - 1 = 0 ,$

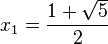
$x_1 = frac{1 + sqrt{5}}{2} ,$

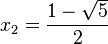
$x_2 = frac{1 - sqrt{5}}{2} ,$

por lo tanto, la solución general es:

$F(n) = A_1 left( frac {1+sqrt{5}} {2} right)^n + A_2 left( frac {1-sqrt{5}} {2} right)^n$

Para hallar el valor de $A 1$ y $A 2$ resolvemos las siguientes ecuaciones:

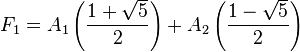
$F_1 = A_1 left ( frac {1+sqrt{5}} {2} right ) + A_2 left ( frac {1-sqrt{5}} {2} right )$

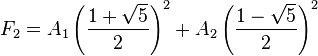
$F_2 = A_1 left ( frac {1+sqrt{5}} {2} right )^2 + A_2 left ( frac {1-sqrt{5}} {2} right )^2$

Entonces:

$A_1 = frac {1} {sqrt{5}}$

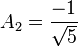
$A_2 = frac{-1}{sqrt{5}}$

La forma cerrada para los números de Fibonacci es:

$F(n) = frac{1}{sqrt{5}} left( left( frac{1+sqrt{5}}{2} right)^n - left( frac{1-sqrt{5}}{2} right)^n right)$

Bilbliografia

http://eisc.univalle.edu.co/cursos/web/material/750084M/1/DiscII_3.pdf